Menteşe teoremi

Geometride, menteşe teoremi, bir üçgenin iki kenarı başka bir üçgenin iki kenarına uyuyorsa ve birincinin iç açısının ikincinin iç açısından daha büyük olduğunda, ilk üçgenin üçüncü kenarının ikinci üçgenin üçüncü kenarından daha uzun olduğunu belirtir. Bu teorem aslında Öklid'in Elemanları Kitabının 24. önermesidir (bazen açık ağız teoremi olarak da adlandırılır). Teorem şunları belirtir:

“ Bir üçgenin iki kenarı, sırasıyla ikinci bir üçgenin iki kenarı ile uyumluysa ve birinci üçgenin iç açısı, ikincisinin iç açısından daha büyükse, o zaman birinci üçgenin üçüncü kenarı, ikincinin üçüncü kenarından daha uzundur.[1] „

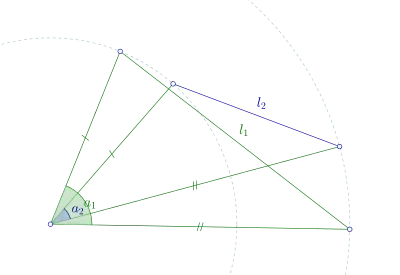
Öklidyen

Menteşe teoremi, Öklid uzayında ve daha genel olarak basit bağlantılı pozitif olmayan kavisli uzay formlarında geçerlidir.

Düzlem Öklid geometrisinden daha yüksek boyutlu Öklid uzaylarına (ör., Dörtyüzlüye -tetrahedra- ve daha genel olarak simplekslere), ortosentrik dörtyüzlü (yani, yüksekliklerin eşzamanlı olduğu dörtyüzlü)[2] için yapıldığı gibi ve daha genel olarak ortosentrik simpleksler için (yani, yüksekliklerin eşzamanlı olduğu simpleksler)[3] genişletilebilir.

Tersi

Menteşe teoreminin tersi de doğrudur: Bir üçgenin iki kenarı, başka bir üçgenin iki kenarıyla eşleşiyorsa ve birinci üçgenin üçüncü kenarı, ikinci üçgenin üçüncü kenarından büyükse, o zaman ilk üçgenin iç açısı, ikinci üçgenin iç açısından daha büyüktür.

Bazı ders kitaplarında teorem ve tersi sırasıyla KAK (Kenar Açı Kenar) Eşitsizlik Teoremi ve KKK (Kenar Kenar Kenar) Eşitsizlik Teoremi olarak yazılmıştır.

Notlar ve Kaynakça
  1. Moise, Edwin; Downs, Jr., Floyd (1991). Geometry. Addison-Wesley Publishing Company. s. 233. ISBN 0201253356.
  2. Abu-Saymeh, Sadi; Mowaffaq Hajja; Mostafa Hayajneh (2012). "The open mouth theorem, or the scissors lemma, for orthocentric tetrahedra". Journal of Geometry. 103 (1): 1-16. doi:10.1007/s00022-012-0116-4.
  3. Hajja, Mowaffaq; Mostafa Hayajneh (1 Ağustos 2012). "The open mouth theorem in higher dimensions". Linear Algebra and Its Applications. 437 (3): 1057–1069. doi:10.1016/j.laa.2012.03.012.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.